概率问题的解题难点往往不在概率公式本身，而是对于题目描述事情的理解，甚至很多概率衍生到一些排列组合的知识点，多知识点结合是概率难题的一大特点。但因为概率问题、排列组合问题都是基于事件完成过程的分析，所以排列组合中的一些原理同样可以应用于概率。下面我们在习题中感受一下。

【例】1.在正方体中任意选择两条棱，则这两条棱相互平行的概率为

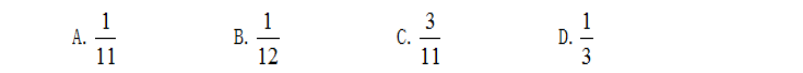
【答案】C.东吴解答：要求两条棱相互平行的概率,可以先固定一条棱,与之平行的棱有3条,可选择的总数为11条,故两条棱相互平行的概率为,故选择C项

由这道题我们可以总结，要求两个事物之间存在特殊关系时，我们可以分步来考虑，先定位其中一个事物，再考虑第二个事物，整个事件的概率马上就能分析清楚。

【例】2.某单位工会组织桥牌比赛，共有8人报名，随机组成4队，每队2人。那么，小王和小李恰好被分在同一队的概率是：

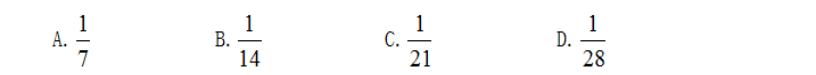
【答案】A。东吴解答：假设小王已经分好队,剩下7个位置小李可以选择,要想和小王一队,只有一种情况,两人被分在同一队的概率是,故选择A项

【例题详解】销售员小刘为客户准备了A、B、C三个方案。已知客户接受方案A的概率为40%。如果接受方案A，则接受方案B的概率为60%，反之为30%。客户如果A或B方案都不接受，则接受C方案的概率为90%，反之为10%，问将3个方案按照客户接受概率从高到低排列，以下正确的是：

A.A>B>C   B.A>C>B   C.B>A>C   D.C>B>A

       这道题目告诉我们什么呢？说是的客户对于小刘提供的ABC三个方案的接受与否的概率信息，让我们解决每种方案接受的概率大小问题。既然是解决概率，我们要看题干告诉的关于接受A、B、C的概率条件。这时我们可以发现，除A以外，BC方案的接受概率都会随着另外的方案去变化，条件较多，我们整理一下：

①接受A为40%；

②接受A后，接受B为60%；

③不接受A后，接受B为30%；

④AB都不接受，接受C为90%；

⑤AB中接受了一种或两种，接受C为10%。

此时我们发现，如果想求B或者C的概率，就要去找到哪些情况下B、C会发生，以B为例，B发生可以是②也可以是③，此时②和③的关系类似于排列组合中的分类，分类的方法数计算用加法，这里概率计算同样用加法，即接受B的概率等于②③概率之和。

   那我们继续分析②，接受A之后，接受B为60%，接受A之后再接受B，在40%的基础上再发生一个60%，类似于排列组合问题中的分步，分步的方法数计算用乘法，这里概率计算同样用乘法，所以②对应的概率为40%×60%=24%。

   同理，③中是不接受A再接受B，概率依旧相乘，为(1-40%)×30%=18%。

   所以接受B的概率为24%+18%=42%。

分析清楚B之后，再来看C，想要接受C可以是④也可以是⑤，分类关系，故接受C的概率为④⑤概率的和。

   在④中，AB都接受，再接受C，分步关系，概率应相乘；AB都不接受其实就是不接受A并且不接受B，概率为60%×(1-30%)=42%，所以④发生的概率为42%×90%=37.8%。

   在⑤中，AB至少接受一个即为AB都接受的反面，概率为1-42%=58%，此时接受C的概率为10%，故⑤发生的概率为58%×10%=5.8%。

   那么接受C的概率就为37.8%+5.8%=43.6%。

此时得出结论，C>B>A，选D选项。

       这道题目中我们分析计算概率的方式，用到了分类、分步中的加乘原理。只要分析清楚题干描述事件发生的方式，结合加乘就可以顺利计算出所求概率。值得注意的是，前提条件，概率能相加的前提是事件之间不交叉即分类关系，概率能相乘的前提是先后完成即分步关系。

       以上是行测中概率问题，你学会了吗?公考并不难，只要肯耐下性子学，东吴教育祝愿您公考顺利。